Chapter 6 介紹了一個猜價格遊戲，並從歷史資料 dataset 中，求出得出要如何才能有最高的期望回饋。本範例中介紹如何使用 KDE 建立 PDF 以及 Likelihood 並得出 Posterior，最後以該數值建立最佳的期望回饋值分佈以得出如何得出最佳 Bid。

ThinkBayes Note

Chapter 6 - Decision Analysis

The Price is Right Problem

假設有一個猜測遊戲，兩名參賽者 (Contestant) 需猜測 showcase 1, 2 中所有物品的價格加總數值，條件如下

  1. 不超過真正的價格，超過就算輸。
  2. 最接近真正價格者獲勝，獲勝者可獲得該 showcase 上的獎品。
  3. 獲勝的參賽者假如與該 showcase 的真實價格差異在 250 內，也可獲得另一個 showcase 的獎品。

以 Bayesian 方式來思考的話，上面的問題可分解為以下部分

  1. 在見到獎品 (Prize) 前，真正價格的機率分佈為何 (Prior)
  2. 見到獎品後，參賽者如何更新心中的預期價格。(Likelihood and Posteriror)
  3. 依照 Posterior distribution 計算出參賽者出價的期望值為多少

第三點即是 Decision analysis 的部分。我們可以依照 Posterior distribution 來求 Expected return 的最大值。

Prior - showcase 實際價格分佈

showcase 2011 與 [showcase 2012](http: //thinkbayes.com/showcases.2012.csv) 為該遊戲在 2011 與 2012 年的統計資料，包含 Showcase 1, 2 的實際價格，參賽者猜測價格（Bid）以及差異數值，因此我們可先由歷史資料中建立真實價格的機率分佈 (Prior)。由於價格為一連續資料，可用 Gaussian Kernel Density Estimation（高斯核密度估計，KDE）從歷史資料分佈建立 Probability Density Functions（機率密度函數，PDF）以產生 Prior distribution。

Probability density functions (PDF)

PDF 是一個連續數值的機率分佈函數，以 Gaussian distribution 為例，

$$f(x|\mu, \sigma^2) = \frac{1}{\sigma\sqrt{2\pi}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$ $$\int_{-\infty}^{\infty}f(x)=1$$

當平均數

$$\mu=0$$

而標準差

$$\sigma=1 $$

時，Gaussian distribution 可寫成

$$f(x)= \frac{1}{\sqrt{2\pi}}\exp(\frac{-x^2}{2})$$

由於 Gaussian distribution 積分為 1，因此上式可是為機率分佈。

PDF 中

$$f(x)$$

求出的值為 Probability Density 而並不是

$$x$$

的機率，需要經過積分才能成為 Probability Mass。

Kernel density estimation (KDE)

KDE 是一種從離散資料建立 PDF 分佈的演算法，假設現有 N 筆資料分別為

$$X=(x_1, x_2, \dots,x_n)$$

，在 x 位置的 Probability density 可計算為

$$f_h(x)=\frac{1}{n}\sum_{i=1}^{n}K_h(x-x_i)=\frac{1}{nh}\sum_{i=1}^{n}K(\frac{x-x_i}{h})$$

其中 K 為 Kernel functino，而 h 為 smooth parameter (called bandwidth)。

以 showcase dataset 為例，實際價格可能為

$$(\dots, 28800, 28868, 28941, 28957, 28958, \dots)$$

這樣的分佈，也就是之前的原始資料

$$X$$

。作者在範例程式中直接使用 scipy library 中的 Gaussian KDE 函式對 showcase 分佈進行計算，可得出每個 showcase 價格的機率分佈。

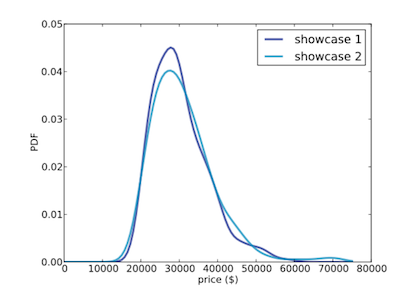prior-showcase showcase dataset 中價格的機率分佈 (Prior)

Modeling the contestants and Likelihood

接下來需考慮兩個問題

  1. 所觀測到的資料 D 為何，以及如何將資料量化。
  2. 如何計算資料的 Conditional Likelihood。

這裡作者使用實際價格（Price）與猜測值（Guess）與之間**差異(Error)**作為觀測到的資料，可定義為。

$$\text{error} = \text{price} - \text{guess}$$

當 Error 為負值時，代表猜測值太高（遊戲失敗）。而在之前的歷史資料有每次遊戲的實際價格(Price)與參賽者下注值(Bid)，因此兩者差異可計算為

$$\text{diff} = \text{price} - \text{bid}$$

因此遊戲歷史資料中的 error 分佈可用 diff 數值建立。假設 error為

$$\mu=0$$

的 Gaussian PDF，標準差

$$\sigma$$

由 diffs 得出。

每個參賽者在猜測價格時，有時候會存在某些策略，如猜測對手可能會超過真正數值就會出價比較低。以及為了避免超過真實價格而猜測價格低等。但作者認為 Modeling 方式是合理的。

Likelihood

當給定一個 Price (Hypothesis) 與 Guess (data)，則 Likelihood 可由之前計算出的 error PDF 計算出來。

$$Likelihood = P(D \mid H) = P(Error \mid Price) = PDF_{error}(diffs)$$

接下來即可計算並得出 Posterior。假如猜測值為 20,000，則最有可能的價格為 24,000

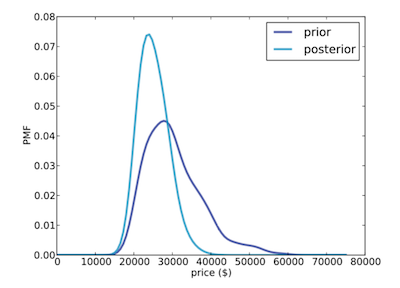guess-2000 猜側價格為 20,000 時，Prior 與 Posterior 的分佈比較

Optimal bidding

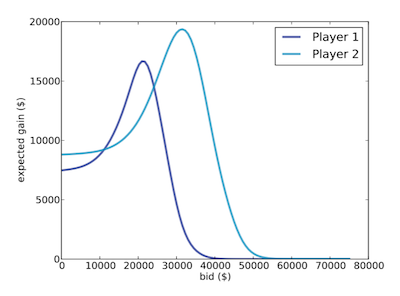
雖然我們可知道到當猜測價格為 20,000 時最有可能的價格是 24,000。但實際上因受到遊戲規則與對手出價等因素影響，又有可能價格的數值不一定可以獲得最高報酬。因此可經由計算 Expected Return 的方式計算不同猜測價格時的期望價格(Expect Gain)是多少。

計算結果如下圖所示，在可看出參賽者 1 (Player 1) 的 Best Guess = 20,000 而參賽者 2 (Player 2) 的 Best Guess = 40,000 的情況下。Player 1 最佳下注為 21,000 而 Expected Return 約 16,700。 Player 2 最佳下注為 31,500 而 Expected Return 約 19,400。可以知道在本範例中，實際上的 optimal bid 數值比最佳猜測值(best guess)低。

prior-showcase

Reference